La controverse Hawking – Bekenstein sur le Trou Noir inspire les chercheurs israéliens

[:fr]
Arthur Robin, auteur pour le BVST, rend hommage à Stephen Hawking, le célèbre physicien décédé en mars 2018, et revient sur « l’affaire du Trou Noir », histoire d’une dispute avec le physicien israélien Jacob Bekenstein (alors étudiant en doctorat) qui mena à une découverte révolutionnaire sur les trous noirs. Ce différent a changé la science des trous noirs et continue à inspirer des chercheurs en Israël, comme le Pr Jeff Steinhauer du Technion.
Revenons tout d’abord là où tout a commencé, à la prestigieuse université de Princeton, aux Etats-Unis. En 1970, le Dr. Stephen Hawking est alors un jeune et talentueux professeur de physique théorique, reconnu pour ses travaux sur les trous noirs, ces objets célestes dont l’existence fut théorisée par Albert Einstein dans sa théorie de la relativité. Dans le même département, un étudiant mexicain, Jacob Bekenstein, alors en doctorat en physique théorique, décide de travailler lui aussi sur les trous noirs aux propriétés si particulières. De ses travaux résultera un conflit qui l’opposera au Dr. Hawking, jusqu’à que ce dernier reconnaisse non seulement son erreur, mais confirme également l’hypothèse de Bekenstein, révolutionnant aux passages la compréhension théorique de ces objets célestes.
Que proposa Jacob Bekenstein ? Il choisit de généraliser la seconde loi de la thermodynamique aux trois noirs et fut l’un des premiers à suggérer que les trous noirs possédaient une entropie définie et que celle-ci était proportionnelle à la taille des trous noirs (la taille ici faisant référence à la surface de son horizon). Seconde loi de la thermodynamique ? Entropie ? Trou noir ? Tout cela peut vous sembler flou au point que le pointeur de votre souris se rapproche dangereusement du bouton de fermeture de votre navigateur internet, mais nous allons vous expliquer ce que cela signifie.
L’entropie permet de décrire l’état d’un système, ou plutôt le nombre d’états que peut prendre un système. Cette valeur est souvent liée à la notion de « désordre », car un objet peut prendre beaucoup plus d’états « désordonnés » que d’états ordonnés, donc les objets ont statistiquement plutôt tendance à être désordonnés qu’ordonnés ; par exemple, mélangez des billes rouges et bleus dans un bol : la probabilité que les billes soient parfaitement séparées par couleur est très faible. Cette notion explique aussi pourquoi, lorsque l’on met un objet chaud en contact avec un objet froid, la chaleur va diffuser de l’objet chaud vers l’objet froid, et non l’inverse : cela est certes intuitif, mais sans que l’on puisse l’expliquer. L’entropie est en fait intimement liée à la température et à l’énergie d’un objet physique.
En bref, un objet physique possède un certain désordre, qui est lié à sa composition et à l’énergie totale contenue dans cet objet. Si l’objet subit une transformation quelconque, cette transformation va impacter le « désordre » des atomes le constituant, de telle façon que la nouvelle valeur de désordre sera identique à la valeur initiale si cette transformation est réversible (i.e. il est possible de revenir à l’état initial, car il n’y a pas de pertes d’énergies « utiles », donc on ne créé pas d’entropie), ou supérieure à l’entropie initiale si la transformation est irréversible (i.e. une partie de l’énergie initiale est « perdue », dans le sens où elle diffuse en dehors de l’objet). La variation d’entropie d’un objet est donc forcément nulle ou positive : c’est la seconde loi de la thermodynamique. Elle peut être négative dans certain cas, mais uniquement localement, c’est-à-dire que l’on peut réduire l’entropie d’un objet, mais que cela implique de créer plus d’entropie autre part (en utilisant une source d’énergie extérieure par exemple). De fait, l’entropie de l’univers est en constante augmentation. Mais revenons à nos moutons (noirs).
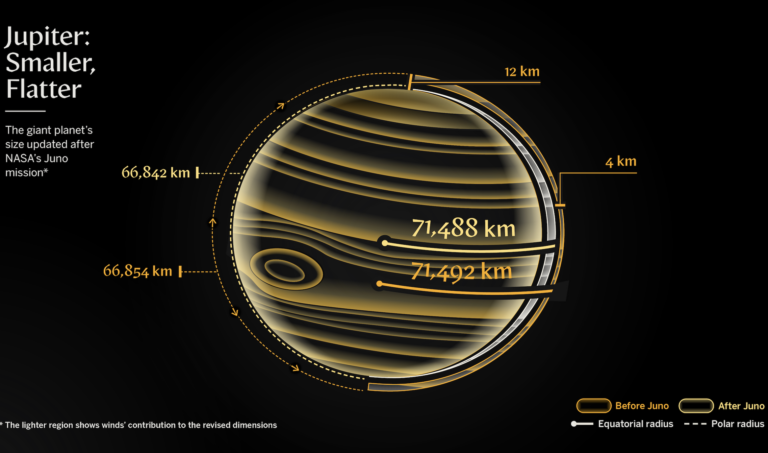
Un trou noir est, selon la relativité d’Albert Einstein, une singularité, un objet infiniment petit au point d’avoir un rayon nul, mais dont la masse est colossal. Cette masse est telle que toutes les molécules passant à proximité peuvent être « happées » par le trou noir et que ces forces d’attractions atteignent à un certain point une telle valeur que les particules de lumière elles-mêmes sont englouties. De ce fait, un trou noir absorbe les particules passant dans sa zone d’influence et n’émet donc aucune particule et notamment aucune lumière, d’où le nom de « trou noir ». De ce fait, la seule « chose » qui sort d’un trou noir est la formidable attraction gravitationnelle qu’exerce celui-ci. Cette attraction est liée aux ondes gravitationnelles, mais il s’agit d’un autre sujet tout aussi passionnant et parfaitement d’actualité (voir la brève de janvier dernier : « Un si précieux signal : les ondes gravitationnelles émises lors de la fusion de 2 étoiles à neutrons », lien en fin d’article).
Or, l’entropie d’un objet physique est, comme on l’a dit ci-dessus, liée à l’énergie et à la température de ce même objet. L’entropie d’un trou noir est donc liée à sa température et à son énergie. Ainsi, lorsque J. Bekenstein suggère qu’un trou noir possède une entropie, cela sous-entend que le trou noir a une énergie et une certaine température. C’est ici que débute le conflit l’opposant au Dr Hawking. En effet, tout corps doté d’une température émet un rayonnement. Or, selon la définition d’un trou noir et des travaux du Dr. Hawking de cette époque, un trou noir n’émet aucun rayonnement. Pourtant, le doute est né et l’idée plantée par J. Bekenstein va peu à peu germer dans l’esprit du Dr. Hawking. Il décide donc de s’atteler à prouver que J. Bekenstein a tort, car rappelons-le, la physique théorique à cette époque est en pleine expansion après les travaux d’Albert Einstein (et elle l’est encore) et que cette propriété des trous noirs n’avait pas encore été étudiée en profondeur.
Or, au fil des calculs (dont nous vous faisons grâce), M. Hawking découvrit quelques années plus tard que J. Bekenstein avait bien raison et que les trous noirs émettaient bien un rayonnement, qu’il décrivit avec précision. Ce rayonnement, purement théorique, fut nommé « rayonnement Hawking-Bekenstein » et la découverte eut un fort retentissement dans le monde de la physique.
Stephen Hawking continua à travailler dans la physique théorique, à sa vulgarisation et à de nombreux autres sujets ; il reçut notamment le prestigieux Prix Wolf en Israël en 1988, récompensant les plus importantes contributions en physique. Il fit tout cela tout en se battant contre sa maladie et ce, jusqu’à son décès le 13 mars 2018.
Jacob Bekenstein devint également un prestigieux physicien en Israël, à l’Université Ben Gourion du Néguev, puis à l’Université hébraïque de Jérusalem. Il obtint de nombreux prix pour ces travaux (dont le Prix Wolf en 2012) et continua ses recherches jusqu’à sa mort en 2015.
Aujourd’hui, une nouvelle génération de physiciens, expérimentaux cette fois, s’attèle à prouver les théories de ces génies de la physique par la preuve de l’expérience. C’est le cas par exemple du Pr Jeff Steinhauer du Technion, qui travaille principalement sur les émissions Hawking-Bekenstein et dont l’équipe a publié de nombreux articles scientifiques sur ce sujet, le dernier dans la prestigieuse revue Nature Physics en 2016.
Sources :
• Article du New York Times sur M. Bekenstein (en anglais)
• Page Wikipédia du Dr. Bekenstein
• Page Wikipédia du rayonnement d’Hawking (la version anglaise est plus complète)
• Page Wikipédia « trou noir »
• Site du Pr Jeff Steinhauer du Technion (en anglais)
En savoir plus :
• Sur la biographie et les travaux de Stephen Hawking (en anglais)
• Page Wikipédia vers L’entropie
• Page Wikipédia vers la thermodynamique et ses lois
• Vidéo explicative sur l’entropie par les Shadok
• Vidéo explicative sur l’entropie (en anglais)
• Brève sur les ondes gravitationnelles
Rédacteur : Arthur Robin, doctorant à l’Université de Tel Aviv pour le BVST
[:en]
In the fall of 1973 Dr. Stephen W. Hawking, who has spent his entire professional career at the University of Cambridge, found himself ensnared in a horrendous and embarrassing calculation. Attempting to investigate the microscopic properties of black holes, the gravitational traps from which not even light can escape, Dr. Hawking discovered to his disbelief that they could leak energy and particles into space, and even explode in a fountain of high-energy sparks.
Dr. Hawking first held off publishing his results, fearing he was mistaken. When he reported them the next year in the journal Nature, he titled his paper simply »Black Hole Explosions? » His colleagues were dazzled and mystified.
Nearly 30 years later, they are still mystified. When they gathered in Cambridge this month to mark Dr. Hawking’s 60th birthday with a weeklong workshop titled »The Future of Theoretical Physics and Cosmology, » the ideas spawned by his calculation and its aftermath often took center stage.
They are ideas that touch on just about every bone-jarring abstruse concept in modern physics.
»Black holes are still fundamentally enigmatic objects, » said Dr. Andrew Strominger, a Harvard physicist, who attended. »In fundamental physics, gravity and quantum mechanics are the big things we don’t understand. Hawking’s discovery of black hole radiation was of fundamental importance to that connection. »
Black holes are the prima donnas of Einstein’s general theory of relativity, which explains the force known as gravity as a warp in space-time caused by matter and energy. But even Einstein could not accept the idea that the warping could get so extreme, say in the case of a collapsing star, that space could wrap itself completely around some object like a magician’s cloak, causing it to disappear as a black hole.
Dr. Hawking’s celebrated breakthrough resulted partly from a fight. He was hoping to disprove the contention of Jacob Bekenstein, then a graduate student at Princeton and now a professor at the Hebrew University in Jerusalem, that the area of a black hole’s boundary, the point of no return in space, was a measure of the entropy of a black hole. In thermodynamics, the study of heat and gases, entropy is a measure of wasted energy or disorder, which might seem like a funny concept to crop up in black holes. But in physics and computer science, entropy is also a measure of the information capacity of a system — the number of bits that it would take to describe its internal state. In effect, a black hole or any other system was like a box of Scrabble letters — the more letters in the box the more words you could make, and the more chances of gibberish.
According to the second law of thermodynamics, the entropy of a closed system always stays the same or increases, and Dr. Hawking’s own work had shown that the hole’s surface area always increased, a process that seemed to ape that law.
But Dr. Hawking, citing classical physics, argued that an object with entropy had to have a temperature, and anything with a temperature — from a fevered brow to a star — must radiate heat and light with a characteristic spectrum. If a black hole could not radiate, it could have no temperature and thus no entropy. But that was before gravity, which shapes the cosmos, met quantum theory, the paradoxical rules that describe the behavior of matter and forces within it. When Dr. Hawking added a touch of quantum uncertainty to the standard Einsteinian black hole model, particles started emerging. At first he was annoyed, but when he realized this »Hawking radiation » would have the thermal spectrum predicted by thermodynamic theory, he concluded his calculation was right.
But there was a problem. The radiation was random, Dr. Hawking’s theory said. As a result, all the details about whatever had fallen into the black hole could be completely erased — a violation of a hallowed tenet of quantum theory, which holds that it should always be possible to run the film backwards and find out the details of how something started — whether an elephant or a Volkswagen had been tossed into the black hole, for example. If he was right, Dr. Hawking suggested, quantum theory might have to be modified. Black holes, he said in his papers and talks in the late 1970’s, were ravagers of information, spewing indeterminacy and undermining law and order in the universe.
»God not only plays dice with the universe, » Dr. Hawking said, inverting the phrase by which Einstein had famously rejected quantum uncertainty, »but sometimes throws them where we can’t see them. » Such statements aroused the attention of particle physicists. Weird as it may be, quantum theory is nonetheless the foundation on which much of the modern world is built, everything from transistors to CD’s, and it is the language in which all of the fundamental laws of physics, save gravity, are expressed. »This cannot be, » Dr. Leonard Susskind, a theorist at Stanford, recalled saying to himself.
It was the beginning of what Dr. Susskind calls an adversarial relationship. »Stephen Hawking is one of the most obstinate people in the world; no, he is the most infuriating person in the universe, » Dr. Susskind told the birthday workshop, as Dr. Hawking grinned in the back row.
In the ensuing 20 years, opinions have split mostly along party lines. Particle physicists like Dr. Susskind and Dr. Gerard ‘t Hooft, a physicist at the University of Utrecht and the 1999 Nobel Prize winner, defend quantum theory and say that the information must get out somehow, perhaps subtly encoded in the radiation. Another possibility — that the information was left behind in some new kind of elementary particle when the black hole evaporated — seems to have fallen from favor.
Relativity experts like Dr. Hawking and his friend the Caltech physicist Dr. Kip Thorne were more likely to believe in the power of black holes to keep secrets. In 1997, Dr. Hawking and Dr. Thorne put their money where the black hole mouth was, betting Dr. John Preskill, a Caltech particle physicist, a set of encyclopedias that information was destroyed in a black hole.
To date neither side has felt obliged to pay up.
Writing on the Wall
Dr. Susskind and others have argued that nothing ever makes it into the black hole to begin with because, in accord with Einstein, everything at the boundary, where time slows, would appear to an outside observer to »freeze » and then fade, spreading out on the surface where it could produce subtle distortions in the Hawking radiation.
In principle, then, information about what had fallen onto the black hole could be read in the radiation and reconstructed; it would not have disappeared.
The confusion had arisen, Dr. Susskind explained, because physicists had been trying to imagine the situation from the viewpoint of God rather than that of a particular observer who had to be either in the black hole or outside, but not both places at once. When the accounting is done properly, he said, »No observer sees a violation of the laws of physics. »
The information paradox made it important for theorists to try to go beyond thermodynamic analogies and actually calculate how black holes store information or entropy. But there was a catch. According to a well-known formula developed by the Austrian physicist Ludwig Boltzmann (and engraved on his tombstone), the entropy of a system could be determined by counting the number of ways its contents could be arranged.
In order to enumerate the possible ways of arranging the contents of a black hole, physicists needed a theory of what was inside. By the mid-1990’s they had one: string theory, which portrays the forces and particles of nature, including those responsible for gravity, as tiny vibrating strings.
In this theory, a black hole is a tangled mélange of strings and multidimensional membranes known as »D-branes. » In a virtuoso calculation in 1995, Dr. Strominger and Dr. Cumrun Vafa, also of Harvard, untangled the innards of an »extremal » black hole, in which electrical charge just balanced gravity.
Such a hole would stop evaporating and would thus appear static, allowing the researchers to count its quantum states. They calculated that the entropy of a black hole was its area divided by four — just as Dr. Hawking and Dr. Bekenstein said it would be.
The result was a huge triumph for string theory. »If string theory had been wrong, that would have been deadly, » Dr. Strominger said.
The success of the Harvard calculation has encouraged some particle physicists to conclude that black holes can be analyzed with the tools of quantum mechanics, and thus that the information issue has been resolved. But others say this has yet to be accomplished — among them Dr. Strominger, who added, »It remains an unsettled issue. »
Degrees of Freedom
Perhaps the most mysterious and far-reaching consequence of the exploding black hole is the idea that the universe can be compared to a hologram, in which information for a three-dimensional image can be stored on a flat surface, like an image on a bank card.
In the 1980’s, extending his and Dr. Hawking’s work, Dr. Bekenstein showed that the entropy and thus the information needed to describe any object were limited by its area. »Entropy is a measure of how much information you can pack into an object, » he explained. »The limit on entropy is a limit on information. »
This was a strange result. Normally you might think that there were as many choices — or degrees of freedom about the inner state of an object — as there were points inside that space. But according to the so-called Bekenstein bound, there were only as many choices as there were points on its outer surface.
The »points » in this case are regions with the dimensions of 10-33 centimeters, the so-called Planck length that physicists believe are the »grains » of space. According to the theory, each of these can be assigned a value of zero or one — yes or no — like the bits in a computer.
»What happens when you squeeze too much information into an object is that you pack more and more energy in, » Dr. Bousso said. But if it gets too heavy for its size, it becomes a black hole, and then »the game is over, » as he put it. »Like a piano with lots of keys but you can’t press more than five of them at once or the piano will collapse. »
The holographic principle, first suggested by Dr. ‘t Hooft in 1993 and elaborated by Dr. Susskind a year later, says in effect that if you can’t use the other piano keys, they aren’t really there. »We had a completely wrong picture of the piano, » explained Dr. Bousso. The normal theories that physics uses to describe events in space-time are redundant in some surprising and as yet mysterious way. »We clearly see the world the way we see a hologram, » Dr. Bousso said. »We see three dimensions. When you look at one of those chips, it looks pretty real, but in our case the illusion is perfect. »
Dr. Susskind added: »We don’t read the hologram. We are the hologram. »
The holographic principle, these physicists say, can be applied to any space-time, but they have no idea why it works.
»It really should be mysterious, » Dr. Strominger said. »If it’s really true, it’s a deep and beautiful property of our universe — but not an obvious one. »
The Frontiers of Beauty
That beauty, however, comes at a price, said Dr. ‘t Hooft, namely cause and effect. If the information about what we are doing resides on distant imaginary walls, »how does it appear to us sitting here that we are obeying the local laws of physics? » he asked the audience at the Hawking birthday workshop.
Quantum mechanics had been saved, he declared, but it still might need to be supplanted by laws that would preserve what physicists call »naïve locality. »
Dr. ‘t Hooft acknowledged that there had been many futile attempts to eliminate quantum mechanics’ seemingly nonsensical notions, like particles that can instantaneously react to one another across light-years of space. In each case, however, he said there were assumptions, or »fine print, » that might not hold up in the end.
Recent observations have raised the stakes for ideas like holography and black hole information. The results suggest that the expansion of the universe is accelerating. If it goes on, astronomers say, distant galaxies will eventually be moving away so fast that we will not be able to see them anymore.
Living in such a universe is like being surrounded by a horizon, glowing just like a black hole horizon, over which information is forever disappearing. And since this horizon has a finite size, physicists say, there is a limit to the amount of complexity and information the universe can hold, ultimately dooming life.
Physicists admit that they do not know how to practice physics or string theory in such a space, called a de Sitter space after the Dutch astronomer Willem de Sitter, who first solved Einstein’s equations to find such a space. »De Sitter space is a new frontier, » said Dr. Strominger, who hopes that the techniques and attention that were devoted to black holes in the last decade will enable physicists to make headway in understanding a universe that may actually represent the human condition.
Dr. Bousso noted that it was only in the last few years, with the discovery of D-branes, that it had been possible to solve black holes. What other surprises await in string theory? »We have no idea how small or large a piece of the theory we haven’t seen yet, » he said.
In the meantime, perhaps in imitation of Boltzmann, Dr. Hawking declared at the end of the meeting that he wanted the formula for black hole entropy engraved on his own tombstone.
It’s All in the Mathematics
When Stephen Hawking startled cosmologists by asserting that energy and matter could leak out of black holes, his calculations did not say how particles escaped from the black hole, only that they could. The only truth is in the mathematics, he says.
According to Heisenberg’s uncertainty principle, a pillar of quantum theory, the so-called vacuum of space is not empty but rather foaming with virtual particles that flash into existence in particle-antiparticle pairs on borrowed energy and then meet and annihilate each other in a flash of energy that repays the debt of their existence.
But if only one member of a pair fell into a black hole, its mate would be free to wander away. To a distant observer it would appear to be coming out of the black hole, and, since the energy for its creation had been borrowed from the black hole’s gravitational field and then not been paid back, the black hole would accordingly appear to shrink.
As the black hole shrank it would get hotter and radiate faster, according to Dr. Hawking’s calculations, until it finally exploded.
The mortality of a black hole was of little practical concern. A typical black hole would last 10^64 years, trillions of times the age of the universe.
[:]